Tag: جولیا

اگر روی یک لایهٔ اسفنج آب بریزیم، آب از میان سوراخ‌ها عبور کرده و راه خود را به زیر اسفنج پیدا می‌کند. حال اگر این اسفنج را به تدریج فشرده کنیم و آزمایش را تکرار کنیم، از یک جایی به بعد، دیگر آبی از آن چکه نمی‌کند. همچنین چکه کردن آب از سقف و درست کردن قهوه با دستگاه قهوه‌ساز هم نمونه‌هایی از تراوش¹Percolation است.

می‌توان مسئله را ساده‌تر کرد و آن را به دو بعد تقلیل داد. یک سطح کاشی‌کاری شده را در نظر بگیرید که به صورت تصادفی، بعضی از کاشی‌ها از جنس مواد رسانا ساخته شده‌اند. فرض کنید این سطح، یک مربع بزرگ \( N \times N \) کاشی است و هر کاشی آن با احتمال \(p\) رسانا است. حال پرسش این است که مقدار \(p\) باید چقدر باشد تا اگر یک اختلاف ولتاژ به دو ضلع آن بدهیم، جریان الکتریکی برقرار شود؟

این مسأله حل تحلیلی ندارد. پس باید دست به دامان آزمایش شویم. اگر به اندازهٔ کافی مقدار \(p\) را تغییر دهیم و آزمایش را تکرار کنیم، می‌بینیم که برای \(p\)های مختلف چنین نموداری داریم.

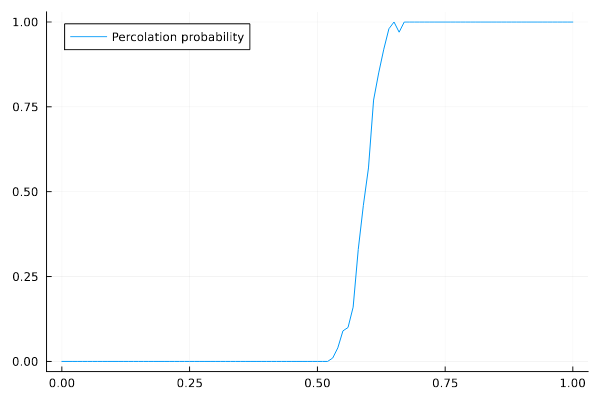
این نمودار تا حدودی نشان می‌دهد که اگر \(p\) از مقدار به خصوصی بیشتر شود، تراوش رخ می‌دهد و اگر \(p\) از آن مقدار کوچک‌تر باشد، شاهد تراوش نیستیم. در رسم نمودار بالا، از ماتریس‌های مربعی با ضلع ۵۰ استفاده شده، حال برای \(N = ۱۰\) و \(N = ۱۰۰\) نیز رسم می‌کنیم.

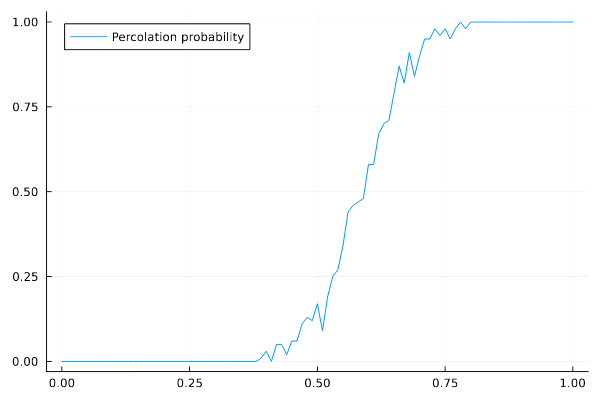
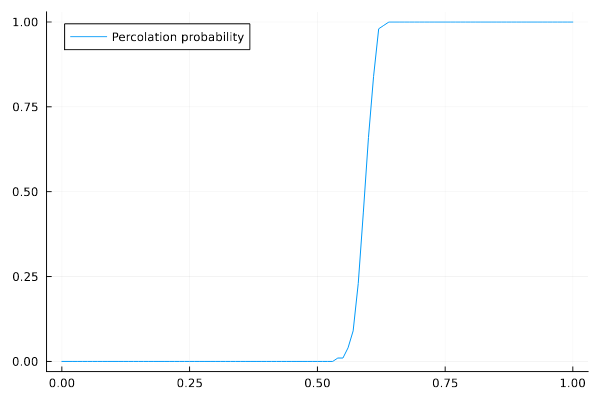
در سیستم‌هایی با اندازهٔ بی‌نهایت، مقدار این کمیت که از حالا به آن \(p_c\) (یا \(p\) بحرانی²critical) می‌گوییم، دقیق می‌شود. برای این سیستم دو بعدی ساده، مقدار \(p_c\) برابر نیم است³هرچند به دلایلی که بر خودم هم معلوم نیست، من عدد \(p_c \approx ۰٫۵۹\). را به دست آوردم..

اما چطور می‌توان تشخیص داد که آیا یک شبکهٔ دو بعدی تراوش می‌کند یا خیر؟ یک الگوریتم ساده و به درد بخور، الگوریتم هوشن-کاپلمن است که شباهت زیادی به رنگ کردن یک شکل بسته در Paint و فتوشاپ (یا جایگزین‌های آزاد و اخلاقی آن‌ها Krita و GIMP) است. این الگوریتم به این صورت است که به خوشه‌های مجاور رنگ‌های تصادفی نسبت می‌دهد و اگر رنگی در سطر بالا و پایین ماتریس، یکسان بود (البته به جز سیاه) به این معنی است که تراوش رخ داده است. به مثال‌های زیر توجه کنید:

نور به جای مایع

یک محیط شفاف را در نظر بگیرید که در بعضی از مناطق آن، اشیاء کدری قرار دارد. اگر از بالا نور بتابانیم به ازای چه مقداری از \(p\) نوری به کف محیط نمی‌تابد؟

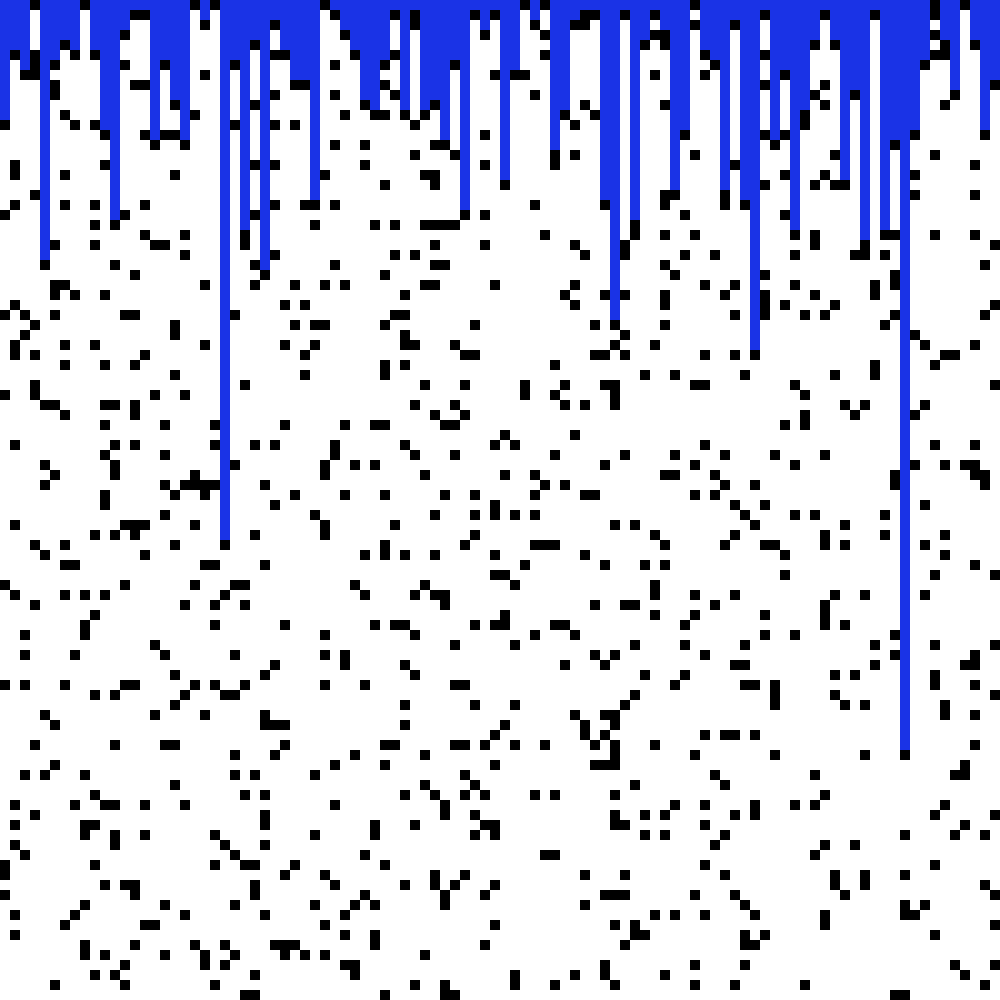
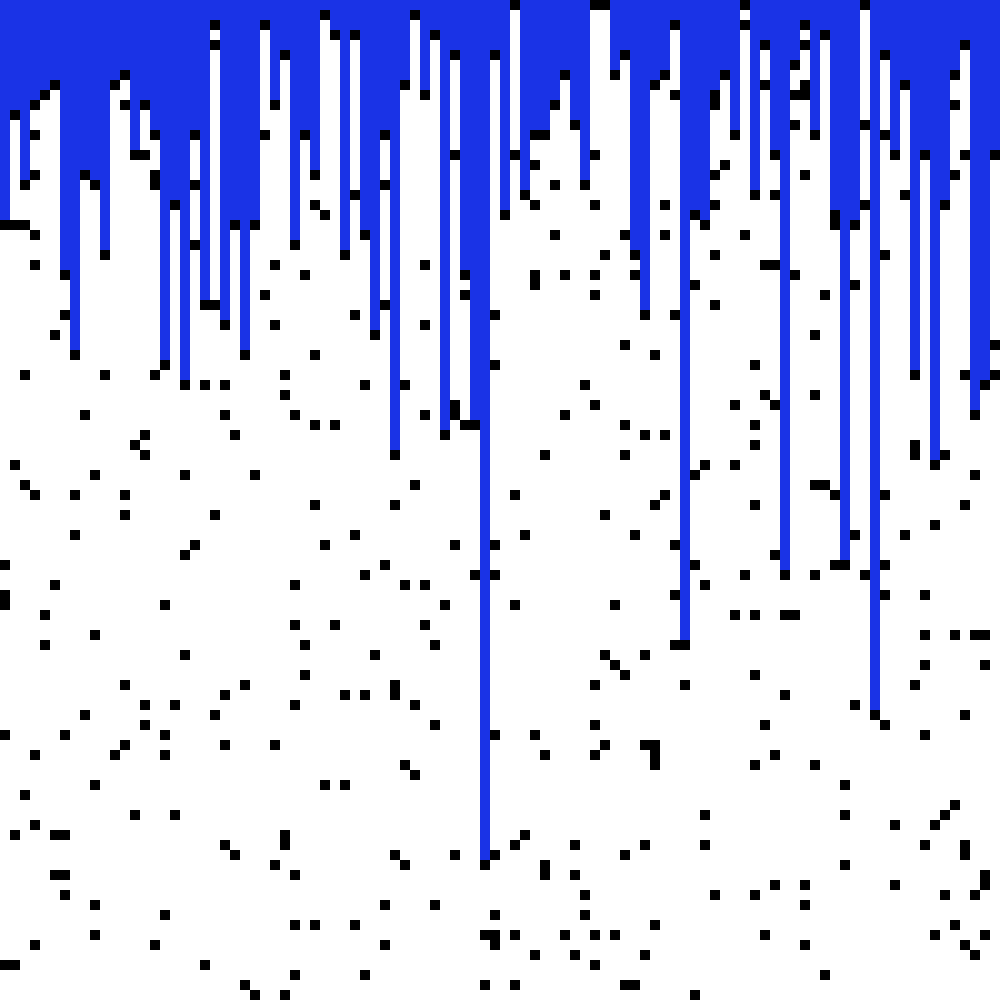
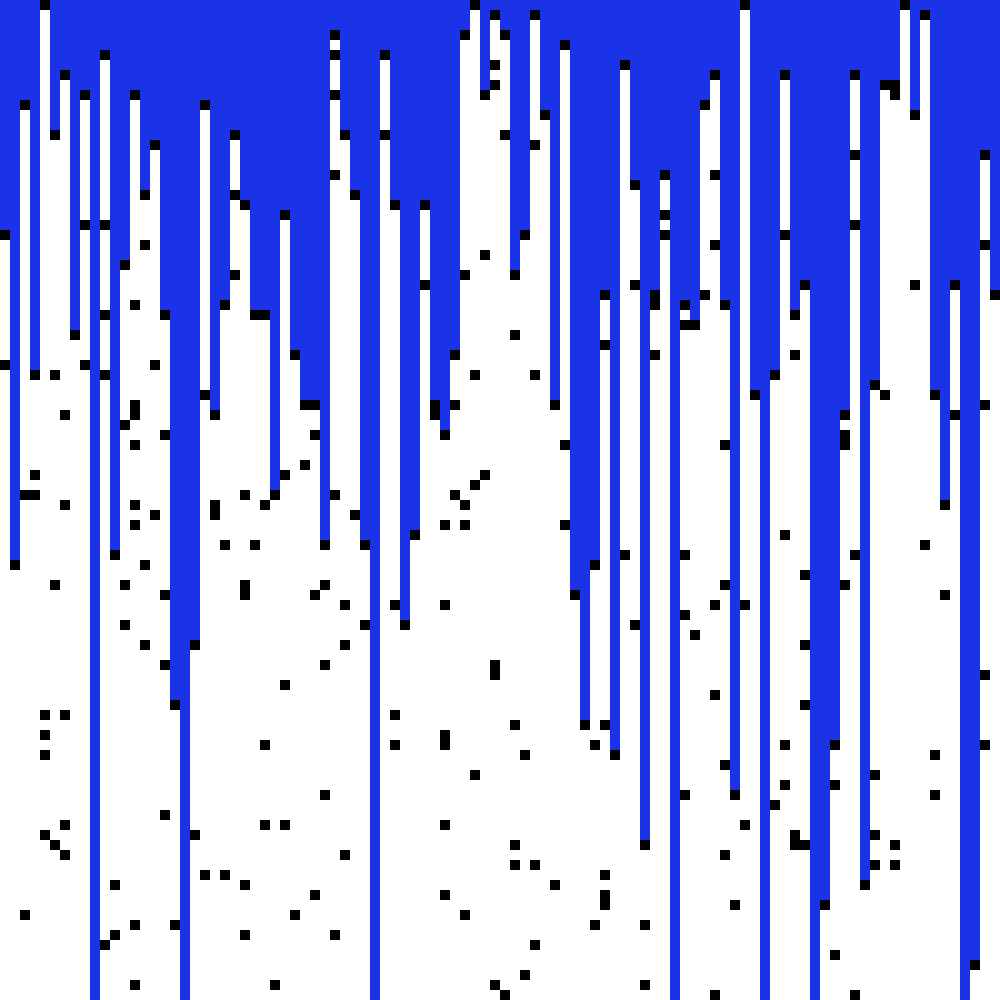
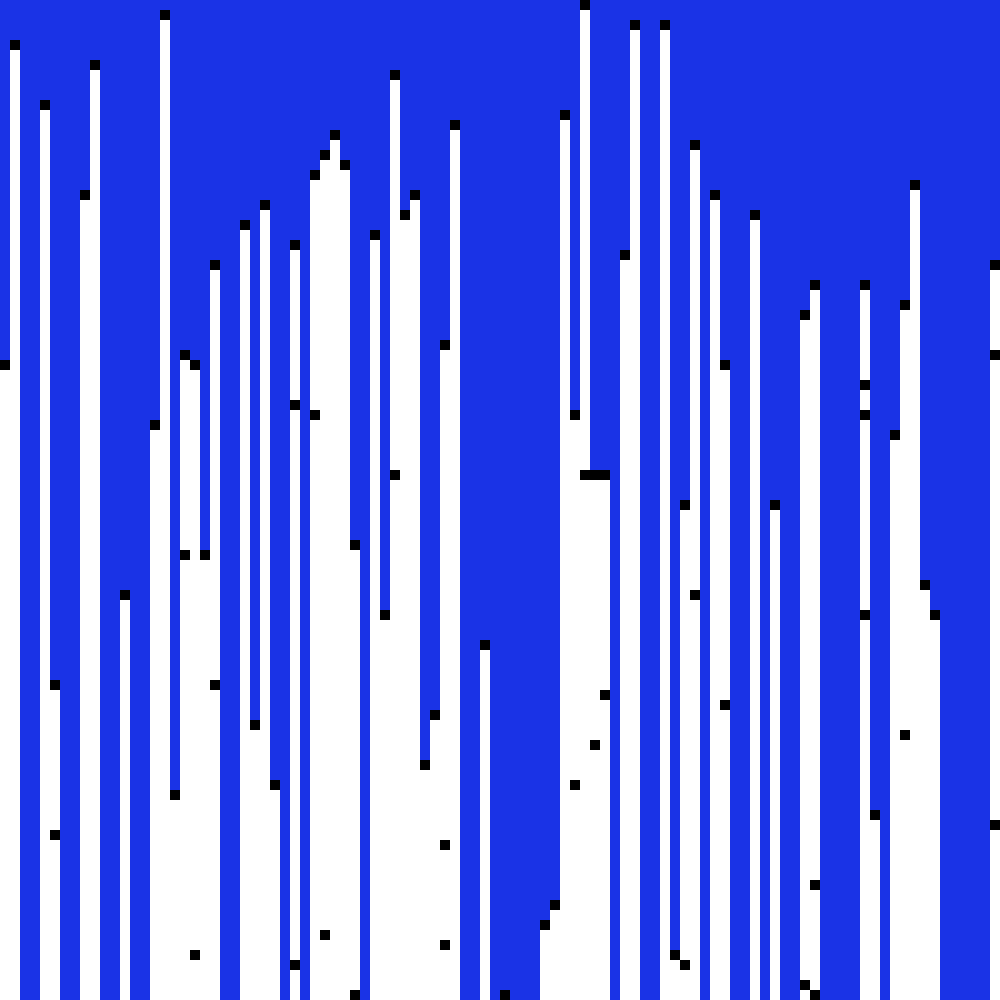
برای این نوع از تراوش، مقدار \(p_c\) بسیار بالاتر است. می‌توان تصور کرد که این نقاط سیاه سنگرهای میدان جنگ است و مناطق سفید نقاطی است که از تیررس دشمن در امان است.

بالاخره تراوش کاربردهای زیادی دارد. گاهی به عمد تعدادی از درختان جنگل‌ها را قطع می‌کنند تا از تراوش آتش به تمام جنگل جلوگیری شود. همچنین در رنگ‌آمیزی مخازن بزرگ سوخت هم برای تخلیهٔ الکتریکی از نظریهٔ تراوش استفاده می‌شود. برای شبیه‌سازی همه‌گیری‌هایی مثل کووید-۱۹ هم چنین است. مثال‌های زیادی برای کاربردهای تراوش در زندگی هست.

مسألهٔ تراوش زمانی برای من جذاب شد که دورهٔ کاربرد کامپیوتر در فیزیک را برداشتم. جلسهٔ پنجم و ششم این دوره در مورد تراوش است و آدم را به وجد می‌آورد. در عنوان این نوشته از «جولیا» نام بردم. جولیا واقعاً عزیز است و تمام کد‌هایی که به خاطر این دوره می‌نویسم (از جمله کدهای مربوط به همین جلسه) را در فراگماگیت همرسانی می‌کنم. برای استفاده از این کدها باید روی سیستم خود جولیا را نصب کرده باشید و روی جولیا هم Pluto Notebook را نصب کنید که آن هم عزیز است.

توجه کنید که به علت کم‌سوادی بنده یقیناً این مطالب و نوت‌بوک‌ها ایرادات و اشتباهات فاحشی دارد که یک نمونهٔ آن \(p_c\) است. اگر علاقمند شدید به جستوجو بپردازید و اگر ایرادی در کار من دیدید حتماً گوشزد کنید که من و دیگرانی که احتمالاً این نوشته را می‌خوانند را از گمراهی و ضلالت نجات دهید.

پایان

عرض کردم پایان

باز هم ادامه می‌دهید؟ پس کامنت بذارید 🙂

حس و حال نوشتن نیست. حتی همین نوشته هم بازخوانی و ویرایش نشده (مثل تقریباً همهٔ نوشته‌های من).

پاورقی

• 1
  Percolation
• 2
  critical
• 3
  هرچند به دلایلی که بر خودم هم معلوم نیست، من عدد \(p_c \approx ۰٫۵۹\). را به دست آوردم.